En la nota Antes de \(\pi\) aproximamos el valor de \(\pi\) mediante la construcción de polígonos de 4, 8, 16, 32 y 64 lados; esto es,
\[2^2\!, 2^3\!, 2^4\!, 2^5 \text{y}\ 2^6\ \text{lados.}\]
Por otra parte, en la nota La raíz de 2 aproximamos el valor de \(\sqrt{2}\) dividiendo el segmento de recta entre 1 y 2 en dos partes, la mitad en dos partes, la cuarta parte en dos partes, etc.; esto es, construimos segmentos de recta de longitud
\[1, \frac{1}{2},\frac{1}{4},\frac{1}{8},\dots\]
que es lo mismo que decir
\[1, \frac{1}{2},\frac{1}{2^2},\frac{1}{2^3},\dots\]
¿Por qué lo hicimos así? Bien pudimos haber utilizado secuencias más simples como
\[4, 5, 6, 7, 8,\dots\quad\text{y}\quad 1, \frac{1}{2},\frac{1}{3},\frac{1}{4},\frac{1}{5},\dots\]
o un poco más complejas como
\[4, 9, 16, 25, 36,\dots\ \text{; esto es,} \ 2^2, 3^2, 4^2, 5^2, 6^2,\dots\]
En otras palabras, ¿por qué construir una secuencia con una base fija y hacer que el exponente crezca, como en
\[2^1\!, 2^2\!, 2^3\!, 2^4\!, 2^5\!,\dots\text{,}\]
en vez de dejar el exponente fijo y hacer que la base crezca, como en
\[1^2\!, 2^2\!, 3^2\!, 4^2\!, 5^2\!,\dots\text{?}\]
Cuenta la leyenda que uno de los primero en usar secuencias donde el exponente crece fue el inventor del ajedrez, quien como regalo por haber inventado un juego que le gustaba tanto a su rey le pidió simplemente

- Un grano de trigo por la primera casilla del tablero.
- Dos granos de trigo por la segunda casilla.
- Cuatro granos por la tercera.
- Ocho granos por la cuarta.
- Etc.
El rey pensó que el juego le había salido muy barato y, antes de que su inventor se arrepintiera y pidiera un premio más grande, mandó a sus sirvientes a que entregaran el premio inmediatamente. Mas tiempo después los sirvientes regresaron para decirle que no podían darle al inventor del ajedrez el premio que quería porque ¡no había tanto trigo en todo el país!
Puedes hacer las cuentas y no te llevará mucho tiempo calcular que el inventor del ajedrez no pedía menos de
¡36,893,488,147,419,103,231 granos de trigo!
Poco más de 36 millones de billones de granos de trigo. Si asumimos que un grano de trigo pesa en promedio 0.06479891 gramos —esto es, que en un kilo de trigo hay 15,432 granos, lo que el inventor del ajedrez pedía era nada menos que
¡2,390,657,818,050.7 toneladas de trigo!
Poco más de dos billones de toneladas de trigo, que equivalen aproximadamente a ¡tres mil veces la producción de trigo en todo el mundo este año! Demasiado, ¿no crees? —por mucho que nos guste el ajedrez.
Como puedes ver, las secuencias exponenciales —llamadas así porque es el exponente el que crece en vez de la base— crecen muy, muy rápido. Tan rápido que rebasan rápidamente a las secuencias lineales, cuadráticas, cúbicas, etc., como lo puedes ver en la siguiente gráfica.
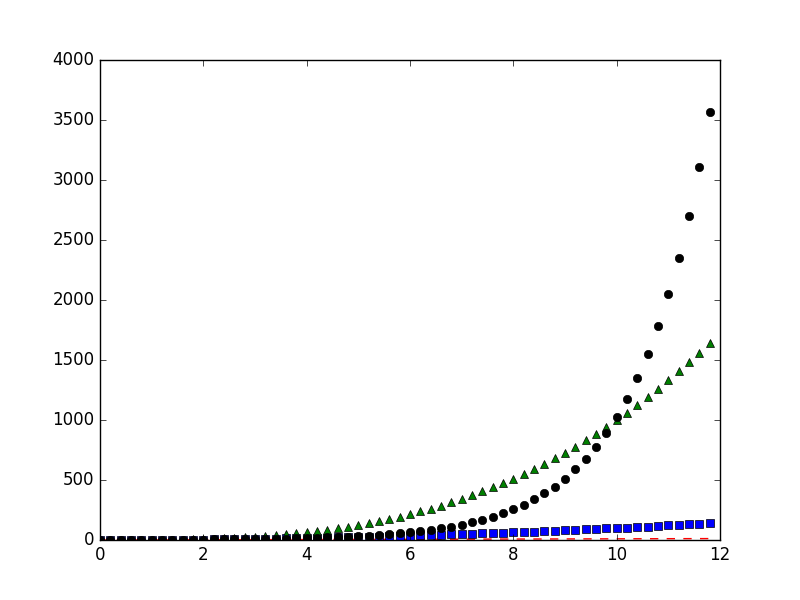
Como puedes ver, la secuencia lineal —\(1, 2, 3, 4, 5,\dots\), representada en la gráfica con segmentos de línea de color rojo— se queda atrás muy pronto, y lo mismo sucede con la secuencia cuadrática —\(1, 2^2\!, 3^2\!, 4^2\!, 5^2\!,\dots\)¸ representada en la gráfica con cuadros azules. La secuencia cúbica —\(1, 2^3\!, 3^3\!, 4^3\!, 5^3\!,\dots\), representada en la gráfica con triángulos verdes— se defiende un poco más, pero no tarda mucho en quedarse atrás de la secuencia exponencia —\(1, 2^1\!, 2^2\!, 2^3\!, 2^4\!,\dots\), representada en la gráfica con círculos negros.
Pero ¿que sucedería si usáramos una secuencia como \(n^{1234567890}\) o con un exponente aún más grande, en vez de simplemente \(n\),\(n^2\!\) o \(n^3\!\)? ¿De todos modos ganaría \(2^n\)?
Órdenes de crecimiento
Una manera de comparar cómo crecen las secuencias es dividiendo sus términos uno a uno, creando así una secuencia nueva y observando qué sucede con ella. Por ejemplo, si dividimos la secuencia lineal entre la secuencia cuadrática obtenemos
\[\frac{n}{n^2} = \frac{1}{n}\]
y en la nota Al infinito y justo ahí encontramos que el límite de esta secuencia, cuando \(n\) crece infinitamente, es cero,
\[\lim_{n\to\infty}\frac{1}{n} = 0,\]
por lo que podemos decir que la secuencia \(n^2\) “le gana” o crece más rápido que la secuencia \(n\). En cambio, si comparamos el crecimiento de la secuencia \(n\) con el crecimiento de la secuencia \(2n\) tenemos que
\[\frac{n}{2n} = \frac{1}{2}\]
y la secuencia que resulta es constante, nunca cambia de \(\frac{1}{2}\), por lo que podemos decir que su límite es \(\frac{1}{2}\),
\[\lim_{n\to\infty}\frac{1}{2} = \frac{1}{2},\]
y en este caso decimos que ni \(n\) ni \(2n\) “ganan” o que ambas crecen igual de rápido —aunque \(2n\) es siempre el doble de \(n\), nunca pasa de ahí.
Como sucede con los límites de las secuencias, sus velocidades de crecimiento son útiles para muchas cosas en matemáticas —¡y en computación!— y les hemos dado un nombre formal: hablamos de órdenes de crecimiento y usamos el símbolo \(O\), como en \(O(n)\), para hablar de la velocidad de crecimiento de una secuencia —de la misma manera en que los karatecas usan cintas de colores.
Escribimos entonces
\[O(n) = O(2n)\quad\text{y}\quad O(n) < O(n^2)\]
para decir que las secuencias \(n\) y \(2n\) crecen a la misma velocidad, pero que la secuencia \(n^2\) crece más rápido que ellas.
En general, si el exponente \(p\) es más grande que el exponente \(q\), entonces la secuencia \(n^p\) crece más rápido que la secuencia \(n^q\) —lo puedes demostrar fácilmente— y entonces
\[O(n^p) > O(n^q).\]
¿Qué podemos decir entonces de la secuencia exponencial? Se sabe —y lo demostraremos en otra nota más adelante— que crece más rápido que cualquier secuencia \(n^p\) sin importar que tan grande es \(p\). Esto es,
\[O(2^n) > O(n^p).\]
Por eso es que la escogimos para calcular el valor de \(\pi\), porque hace que el número de lados del polígono inscrito crezca muy rápido, y por eso la escogimos para calcular el valor de \(\sqrt{2}\), porque hace que el tamaño del segmento de recta donde encerramos a \(\sqrt{2}\) disminuya muy rápido. Por eso la escogió también el inventor del juego de ajedrez para obtener su premio 😉


[…] de las secuencias lineal, cuadrática, cúbica y exponencial, que observamos punteadas en la nota Crecimiento exponencial, ahora se ven como una una línea […]
[…] de las secuencias lineal, cuadrática, cúbica y exponencial, que observamos punteadas en la nota Crecimiento exponencial, ahora se ven como una una línea continua, porque están definidas para todos los […]