A lo largo de miles de años de habitar el planeta Tierra, los seres humanos han modificando tanto su entorno de vida que nos resulta muy difícil imaginar cómo es que se vivía antes, cuando no había teléfonos celulares ni Internet, ni televisiones, ni automóviles, ni luz eléctrica, ni escuela… Algunos artistas nos han dejado películas, documentales y libros donde nos describen cómo se vivía antes —por ejemplo, en el libro y película Orgullo y prejuicio (Pride and Prejudice) nos describen cómo se vivía a principios del siglo XIX— pero no pueden darnos todos los detalles.
Como las matemáticas no son muy taquilleras 🙁 , es muy difícil que encontremos un video o libro donde nos muestren o expliquen cómo era antes, cuando se desconocía que Pi (π) existía. Por ejemplo, cómo es que se calculaban el área y el perímetro de los círculos si se desconocían sus respectivas fórmulas:
$$A = \pi r^2$$
y
$$P = 2\pi r$$
Se sabe que tanto en China como en la India y Egipto se descubrió que π existía y se logró calcular su valor con cierta precisión (3.1…) hace más de tres mil años; pero fueron los griegos (Arquímedes, para ser precisos) quienes se preocuparon por demostrar que existía y calcular su valor con mayor precisión, hace poco más de 2250 años, cuando no existía todavía ni siquiera lo que ahora vemos en ruinas (salvo partes de la Muralla China y las grandes pirámides de Giza, en Egipto, que si son muy, muy antiguas).
Acercándonos a π
Si dibujas un círculo de radio arbitrario, al que le llamaremos r, trazas una línea que lo atraviese por su centro y luego trazas otra línea que también lo atraviese por su centro y que sea perpendicular a la otra —lo puedes hacer con escuadras, con regla y compás, o en la computadora con GeoGebra— obtendrás algo como lo que se presenta abajo.
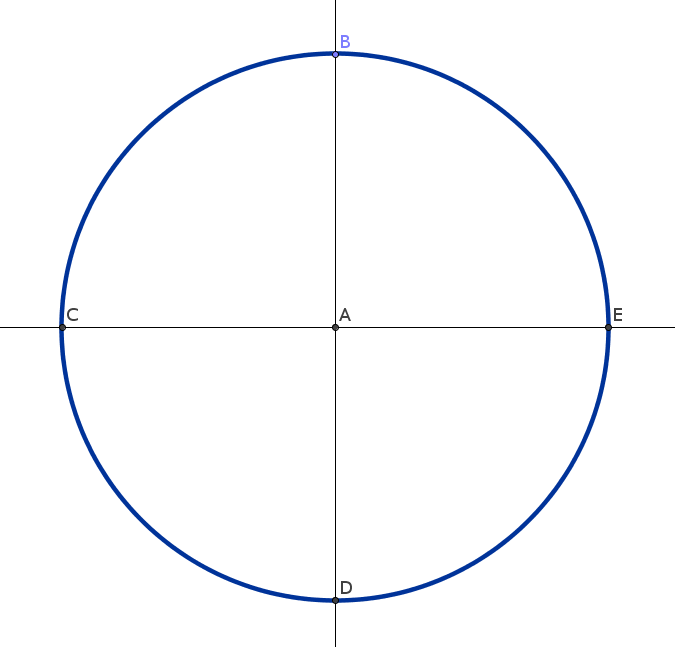
Si unimos los puntos consecutivos en la circunferencia (B con C, C con D, D con E y E con B) obtenemos un cuadrado —esto lo sabemos porque las diagonales son del mismo tamaño (dos veces el radio), son perpendiculares y se cruzan por el centro. Para medir sus lados, podemos trazar una perpendicular desde el centro del círculo a uno de ellos y usar el Teorema de Pitágoras.
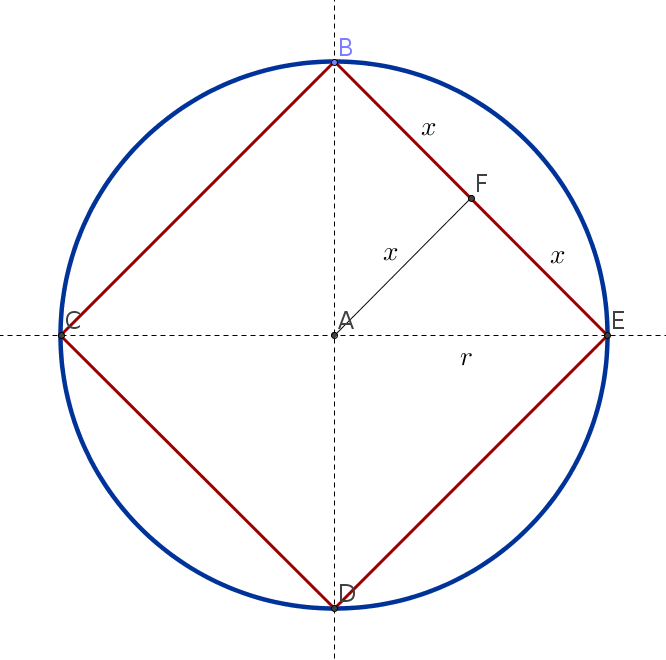
$$\begin{array}{c}
x^2 + x^2 = r^2\\
2x^2 = r^2\\
\displaystyle x = \frac{r}{\sqrt{2}}\\
\displaystyle \overline{EB} = 2x = 2\frac{r}{\sqrt{2}}\\
\overline{EB} = \sqrt{2}r
\end{array}$$
El perímetro del cuadrado es entonces
$$P_4 = 4\sqrt{2}r,$$
y si cambiamos el radio de la circunferencia por su diámetro, tomando en cuenta que el diámetro de una circunferencia está formado por dos radios,
$$d = 2r,$$
entonces
$$P_4 = 2\sqrt{2}d.$$
Es nuestra primera aproximación al perímetro del círculo —esto es, la longitud de su circunferencia— y también nos da una primera aproximación al valor de π:
$$\pi \approx 2\sqrt{2} = 2.8284…$$
Nuestra primera aproximación está todavía muy lejos de lo que sabían los matemáticos chinos hace 3,000 años 🙁 de modo que tendremos que acercarnos más. Para ello prolongaremos la línea \(\overline{AF}\) hasta cruzar el círculo, marcaremos el punto de cruce y lo uniremos tanto con B como con E. Haremos la misma construcción en los otros tres lados del cuadrado. ¡El resultado es un octágono regular!
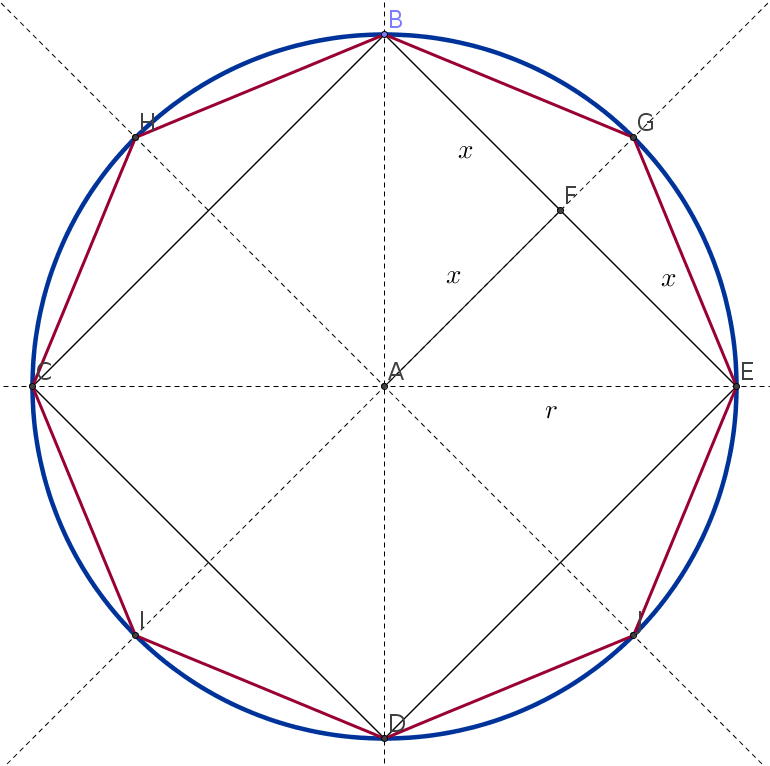
Como en el caso del cuadrado, podemos usar el Teorema de Pitágoras, esta vez en el triángulo BFG, para calcular la longitud de los lados del octágono:
$$\begin{array}{rl}
{\overline{GB}}^2 =& x^2 + {\overline{FG}}^2\\
=& x^2 + (r – x)^2\\
=&\displaystyle {\left(\frac{r}{\sqrt{2}}\right)}^2 + {\left(r – \frac{r}{\sqrt{2}}\right)}^2\\
=&\displaystyle {\left(\frac{r}{\sqrt{2}}\right)}^2 + {\left(\frac{r(\sqrt{2}-1)}{\sqrt{2}}\right)}^2\\
=&\displaystyle \frac{r^2}{2}(1 + 2 – 2\sqrt{2} + 1)\\
=&\displaystyle \frac{r^2}{2}(4 – 2\sqrt{2})\\
=&\displaystyle (2 – \sqrt{2})r^2\\
\overline{GB} =& \sqrt{2-\sqrt{2}}r
\end{array}$$
El perímetro del octágono es entonces
$$P_8 = 8\sqrt{2-\sqrt{2}}r = 4\sqrt{2-\sqrt{2}}d$$
y con ello tenemos nuestra segunda aproximación a la longitud de la circunferencia y, al mismo tiempo, al valor de π:
$$\pi\approx 4\sqrt{2-\sqrt{2}} = 3.0614…$$
Mucho mejor ¿no crees? aunque todavía un poco lejos de los egipcios de hace tres mil años 🙁 . Sin embargo, hemos descubierto un método que nos permite calcular la longitud de la circunferencia y el valor de π con tanta precisión como queramos. Si no nos gusta el resultado con el octágono, podemos construir un polígono de 16, 32, 64, o \(2^n\) lados, donde \(n\) sea el número que queramos —de hecho, con uno o dos polígonos más te darías cuenta de que las fórmulas resultantes tienen un patrón que permite saber cuáles son las que siguen sin construir los polígonos correspondiente 😉 ,
$$\begin{array}{rl}
P_4 =& 2\sqrt{2}d\\
P_8 =& 4\sqrt{2-\sqrt{2}}d\\
P_{16}=&8\sqrt{2-\sqrt{2+\sqrt{2}}}d\\
P_{32}=&16\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2}}}}d\\
P_{64}=&32\sqrt{2-\sqrt{2+\sqrt{2+\sqrt{2+\sqrt{2}}}}}d\\
\dots
\end{array}$$
Los valores aproximados de π a partir de los primeros cinco polígonos (4, 8, 16, 32 y 64 lados, respectivamente) son los siguientes:
| Número de lados | Valor aproximado de pi |
|---|---|
| 4 | 2.8284… |
| 8 | 3.0614… |
| 16 | 3.1214… |
| 32 | 3.1365… |
| 64 | 3.1403… |
En cada caso, el perímetro del círculo se aproxima multiplicando su diametro por una constante, cuyos dígitos van quedando cada vez mejor definidos —primero el 3 queda fijo, luego el 1, y así sucesivamente— lo cual sugiere que π realmente existe y que podemos acercarnos a ella tanto como sea necesario. Este fue un gran descubrimiento de Arquímedes, que ahora tú compartes.
Bibliografía
Número π. (2016, 25 de marzo). Wikipedia, La enciclopedia libre. Fecha de consulta: 00:19, marzo 27, 2016.
Créditos
La imagen destacada fue obtenida de Pixabay. Los diagramas fueron creados usando Geogebra.
Posdata
Hay varias afirmaciones en el texto de esta nota que, si bien son ciertas, no se demuestran, para simplificar la redacción y llegar más rápido y claramente a los puntos importantes; pero la mayor parte de ellas no sin difíciles de demostrar.
- ¿Puedes identificar cuáles?
- ¿Puedes demostrar que son ciertas?
También es posible aproximar el diámetro de la circunferencia construyendo polígonos “por fuera”. De hecho, la combinación de los dos métodos produce mejores resultados incluso con polígonos de pocos lados.
- ¿Puedes desarrollar la aproximación desde afuera?
- ¿Cómo integrarías los dos métodos para obtener más rápido mejores resultados?
Este post participó en la Edición 8.3 del Carnaval de Matemáticas cuyo anfitrión fue el Blog Semillas.

[…] la nota anterior (Antes de π) hicimos uso de la raíz de 2 para calcular el valor de π con diferentes grados de […]
[…] la primera nota de este blog, Antes de Pi ((pi)), se presenta una manera de aproximar el valor de (pi) tanto como sea necesario mediante la […]
[…] la nota Antes de (pi) aproximamos el valor de (pi) mediante la construcción de polígonos de 4, 8, 16, 32 y 64 […]
[…] la nota Antes de (pi) aproximamos el valor de (pi) mediante la construcción de polígonos de 4, 8, 16, 32 y 64 […]
[…] la primera nota de este blog, Antes de Pi ((pi)), se presenta una manera de aproximar el valor de (pi) tanto como sea necesario mediante la […]
[…] la nota anterior (Antes de π) hicimos uso de la raíz de 2 para calcular el valor de π con diferentes grados de […]