Hace ya varias semanas mi hermano compartió una imagen en Facebook en la que se plantea el siguiente problema:

En principio, se trata de una especie de reto a la creatividad que me recuerda mucho al problema planteado en la conferencia de Don Tilman a los padres de niños con síndrome de Asperger en la novela El proyecto esposa (The Rosie Project). Sin embargo, se presta muy bien para una aproximación matemática —que no por ser matemática es menos creativa.
Veamos el problema desde arriba, como un matemático. Desde esta perspectiva, las manzanas se convierten en círculos y el cuchillo en una línea recta.
Por la manera en que hemos acomodado las manzanas, una línea (cuchillo) horizontal no es una solución, porque siempre se tendrá una manzana completa y otra partida en dos: definitivamente, no se repartiría por igual. De modo que tiene sentido pensar en las otras dos opciones: una línea vertical o una línea inclinada. El resultado son las tres situaciones que se plantean a continuación:
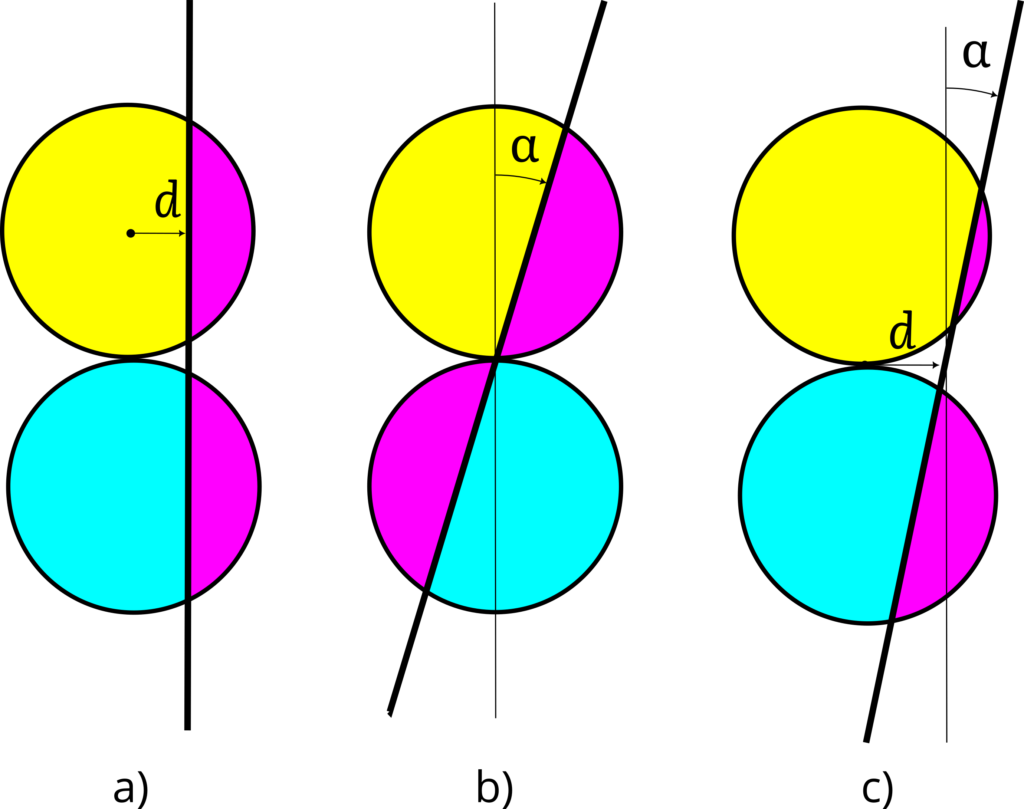
En la situación (a), de corte vertical, el área violeta vale cero si la distancia \(d\) es mayor que el radio de los círculos y va creciendo conforme el valor de \(d\) se va acercando a cero, hasta tener el doble de tamaño que las áreas amarilla y azul, de modo que debe haber un valor de \(d\) en las que las tres áreas tengan el mismo tamaño. En la situación (b) ocurre lo mismo, pero con el ángulo \(\alpha\). Si el ángulo es cero, el tamaño del área violeta es el doble que el de las áreas amarilla y azul, pero si el ángulo es 90°, su tamaño es cero. Finalmente, la situación (c) combina las dos anteriores, pero ¿existe una solución con \(d > 0\) y \(\alpha > 0\)? ¿Puedes encontrar los valores adecuados de \(d\) y \(\alpha\) para los tres casos?
Claro, el modelo anterior tiene un pequeño problema: ¡se asume que las manzanas son planas! Un modelo más real trabajaría con esferas en vez de círculos y un plano en vez de línea recta. Sin embargo, se mantienen las mismas tres situaciones y podrían encontrarse las respuestas correspondientes. ¿Te animas?
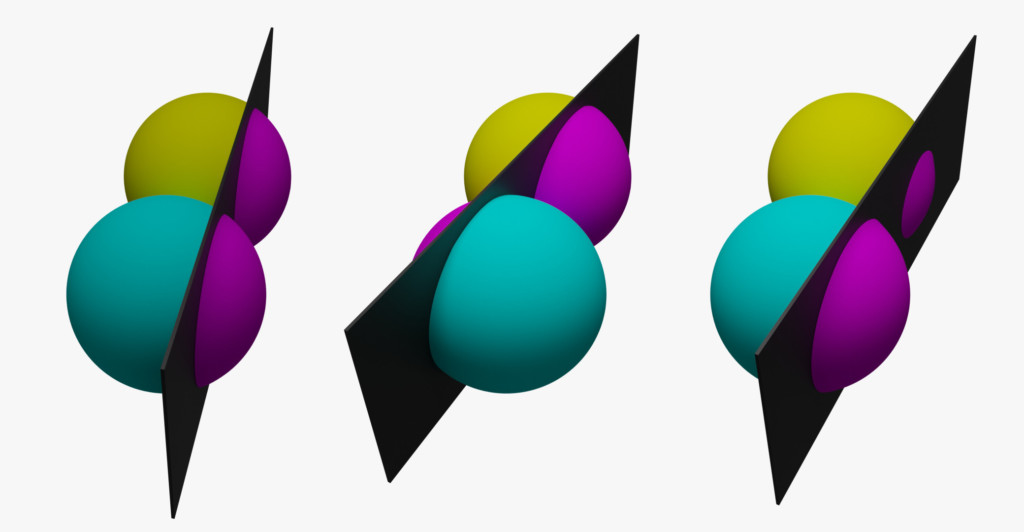


acuchillan a uno de los niños y listo
Efectivamente. De hecho, a esta “solución” es a la que se hace referencia en el primer párrafo de la nota.