El 23 de febrero de 2015 se publicó una nota titulada Copia barata en el blog Desde el IGCAAV, en la cual se da crédito al posicionamiento crítico de una alumna sobre las matemáticas y se planteó la necesidad de darle una respuesta apropiada, bien fundada, no una basada en el criterio de autoridad, sin mayores explicaciones —por considerarlas difíciles para ella— como suele suceder en el salón de clase.
El contenido de este sitio es consecuencia de los intentos por darle respuesta al planteamiento de esa alumna, que se interpretó como se reproduce a continuación (con algunos ajustes).
Copia barata
El último día de enero mi alumna llegó a la conclusión de que
las matemáticas son una copia barata de la realidad.
Hizo su comentario sonriendo, como si fuera una travesura y solamente para ver cómo reaccionaba yo, como Profesor de Matemáticas (así, con mayúsculas). Sin embargo, lo que hice fue contestarle que tenía toda la razón, y a continuación explico por qué.
Tomemos como ejemplo el caso del nautilo, una especie de molusco que es considerado una reliquia de la evolución de las especies en nuestro planeta.

Fuente: Wikipedia, La enciclopedia libre (Nautilus)
El nautilo suele ser un ejemplo muy bonito cuando atendemos el tema de la razón dorada (o número áureo), para lo cual lo aislamos de su hábitat, lo separamos de su concha, tiramos el bicho y nos quedamos solamente con ésta, para luego partirla por la mitad por lo más ancho y observar su interior.

Fuente: Wikipedia, La enciclopedia libre (Número áureo).
Claro, lo que realmente nos interesa es la forma, no su material ni cuáles fueron las fuerzas —físicas, químicas o biológicas— que le dieron forma. Así que pasamos de la concha a la foto de la concha y de ahí a su versión en blanco y negro.

Fuente: Pinterest.
Estudiamos la forma de espiral de la concha, la separamos de sus detalles (sus segmentos, los tonos de gris) y la usamos para inferir o ilustrar el concepto de la espiral dorada.
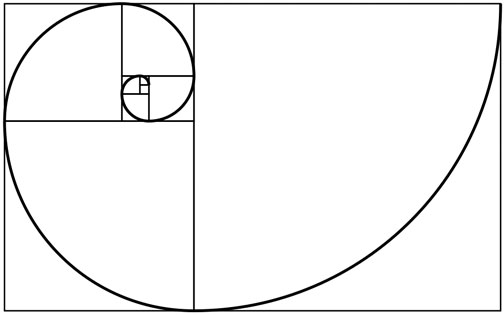
\[r = ae^{\phi\theta}\]
Fuente: Wikipedia, La enciclopedia libre (Espiral dorada)
Claro, si comparamos a un nautilo vivito y nadando con la última imagen, pues sí, podríamos decir que esta última es una “copia barata” del primero, ya que hemos perdido casi toda la riqueza del ser vivo para quedarnos con una forma abstracta.
Fuente: YouTube (Nautilus)
¿Qué podemos decir, en este caso, a favor de las matemáticas?
Poco, realmente, si nos limitamos a las explicaciones tradicionales de que “pero te van a servir”, “son importantes para la vida” o, peor, “sí, pero tienes que aprobarlas para seguir tus estudios”. Al contrario, necesitamos mostrar la belleza del conocimiento humano, incluyendo el de las matemáticas, así como su útilidad y manera de uso en casos concretos.

Recientemente he estado leyendo sobre complejidad, de autores como Edgar Morin y Rolando García, y me doy cuenta que la afirmación de mi alumna —ella sin saberlo, o quizás intuyéndolo— es congruente con la visión de complejidad que Morin presenta en su libro Introducción al pensamiento complejo (1990, edición original en francés):